8.1 最优的判别器策略

我们的目标是在函数空间针对\(D(x)\)最小化以下方程：

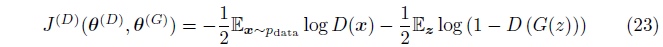
Equation 23

首先假设\(p_{data}\)和\(p_{model}\)是全局非零的。 如果没有此假设， 那么在训练过程中有些点将永远不会被访问到， 并且会出现不被定义的行为。

为了最小化关于\(D\)的\(J^{(D)}\)，我们给出一个针对\(D(x)\)的导数， 并且设此导数为零：

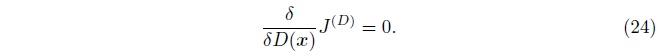
Equation 24

通过解此方程， 可以得到

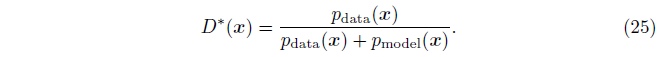
Equation 25

估计此比值是GAN的核心的近似机制，图35展示了此过程。

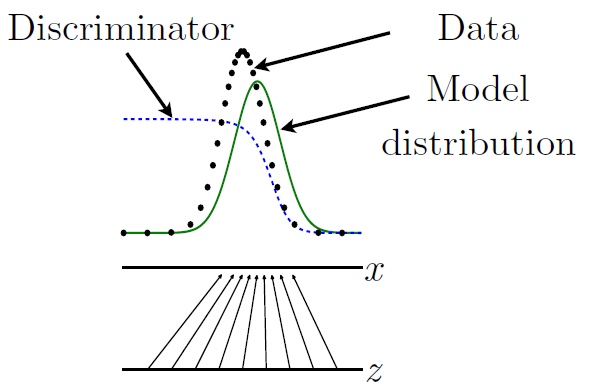
Figure 35

图35： 展示了判别器如何估计密度的比值。 在这个例子中， 为了简化起见， 我们假设\(z\)和\(x\)是一维的。 从\(z\)到\(x\)（黑色箭头所指）的映射是不均匀的（non-uniform）因此\(p_{model}(x)\)（绿色的曲线）在\(z\)的值密度大时会比较大。 判别器（蓝色虚线）估计数据密度（黑点）和模型密度与数据的和的比值。 判别器输出大的地方， 模型密度就比较低， 并且判别器输出比较小的地方，模型密度比较高。 生成器通过不断的学习使判别器的输出上升来产生更好的模型密度； 每一个\(G(z)\)的值应该朝着提高\(D(G(z))\)的方向慢慢移动。 此图来此Goodfellow et al. (2014b).

[关于详细解法，请参考Goodfellow的2014年的文章中的证明（见以下附加图）]

Figure addfig01

附加图： 此图为详细的解的过程， 此图来自Goodfellow et al. (2014b)

8.2 游戏的梯度下降

  • 价值函数（方程式26）可能是最简单的带鞍点的连续函数。

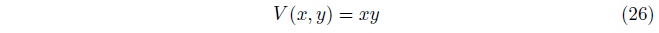
    Equation 26

    通过在三个维度上观察此价值函数， 我们可以很好的理解这个游戏， 如图36。

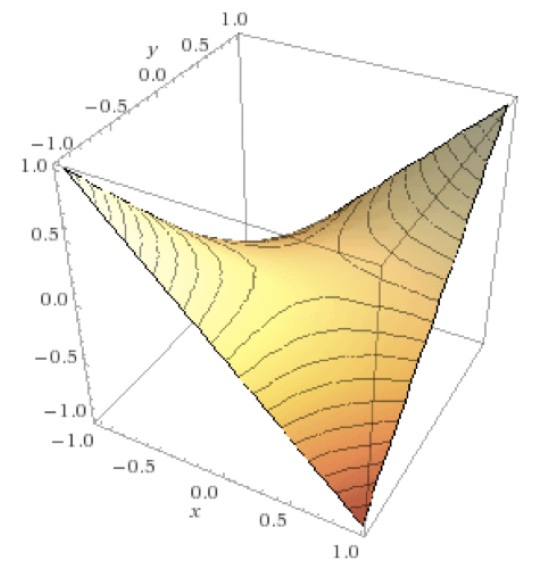
    Figure 36

    图36： 价值函数\(V(x,y)=xy\)的三个维度的展示图， 这是一个典型的有鞍点的函数例子（在x=y=0时）。

    通过三个维度的视角清晰的展示了存在一个鞍点，在\(x=y=0\)。 这是此游戏的平衡点。 我们也可能通过解方程的导数等于零，来得到这个点。

    不是每一个鞍点都是平衡点，是鞍点的要求是： 当我们对一个玩家的参数进行极小的扰动时，此玩家的损失不减少。 这个游戏中的鞍点就满足这个要求。 有些时候可能会是病态的平衡，比如说当将一个玩家的参数固定以后， 另一个玩家的价值函数将会成为一个常量。

  • 为了求解这个梯度下降的轨迹， 首先求导数， 然后发现，

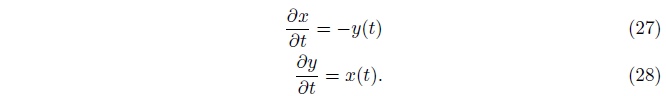
    Equation 27

    对公式28求微分，我们得到

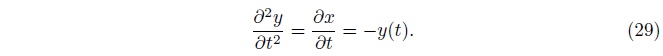
    Equation 29

    这个形式的微分方程是一个正曲线为基函数的方法。 通过解对应边界条件的系数，我们得到

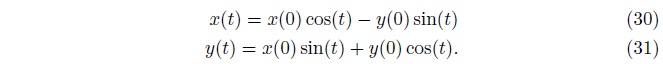
    Equation 30

    优化的轨迹变动会依据一个圆形的轨道， 如图37所示。 换句话说， 同步梯度下降使用一个极小的学习率时，将会进入永远的进入一个以初始化值为半径的平衡的圆轨迹中。 当使用一个大的学习率， 同步梯度下降可能进入到一个螺旋形（也就是外表面）中。 所以， 同步梯度下降将永远不会达到平衡。

    对于有些博弈游戏， 同步梯度下降是可以收敛的， 但是对另外一些， 比如此练习的问题， 是不收敛的。 对于GAN， 没有理论上的证明是否同步梯度下降是否收敛。 挑战这个理论问题， 并且开发算法来保证收敛，仍然是一个很重要的待研究的课题。

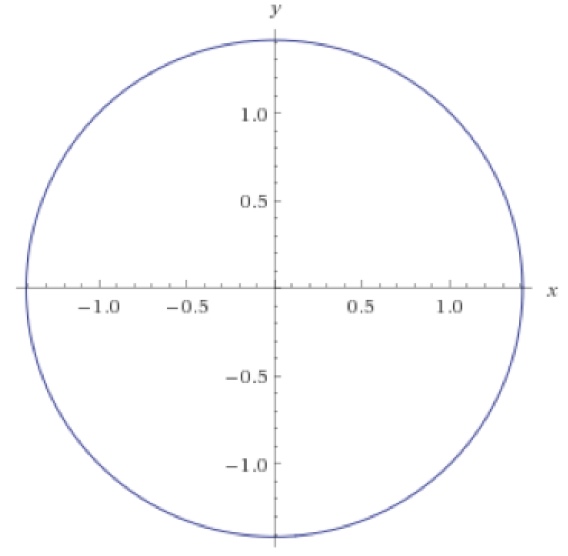
    Figure 37

    图37： 对于\(V(x,y)=xy\)， 当同步梯度下降使用一个很小的学习率时将进入一个不明确常量的半径的轨迹中去, 而不是到达平衡的状态\(x=y=0\)。

8.3 GAN框架中的最大似然

我们希望找到一个函数\(f\), \(f\)的期望梯度是

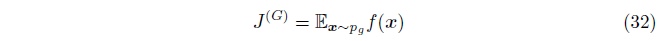
Equation 32

我们希望\(f\)的期望梯度等于\(D_{KL}(p_{data}\|p_{g})\)的期望梯度。

首先将KL散度对\(\theta\)求导，

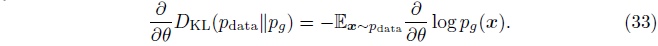
Equation 33

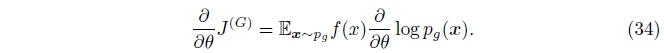
现在我们希望找到\(f\)使方程32的导数与方程33的导数一致。 对方程32求导， Equation 34

为了得到此结果，我们做两个假设：

  1. 假设\(p_g(x) \geq 0\)在全局成立， 那么我们可以使用等式\(p_g(x)=exp(log p_g(x))\).
  2. 假设我们可以使用Leibniz规则来交换微分和其和的顺序 （特别的， 函数和他的导数是连续的， 并且函数对无限大的\(x\)值是不存在的。）

我们看到\(J^{G}\)的导数和我们希望的非常接近； 唯一的问题是， 我们的期望通过从\(p_g\)中采样来计算的，但是我们希望他通过从\(p_{data}\)中采样时来计算。 我们可以通过使用一个很重要的采样技巧该修改此问题； 通过设定 \(f(x)=\frac{p_{data}(x)}{p_g(x)}\)， 我们可以为来自每个产生样本的对导数的贡献重新设置权重， 来弥补因为从生成器采样而不是从真实数据中的问题。

需要注意的是，当构建\(J^{(G)}\)时，我们必须复制\(p_g\) 到\(f(x)\) 从而\(f(x)\)对\(p_g\)的参数的导数为0。 幸运的是， 当我们得到\(\frac{p_{data}(x)}{p_g(x)}\)的值时, 这将会自然的发生。

从8.1章中，我们已经知道了判别器估计希望的比值。 通过数学推导， 我们可以得到一个数字的稳定的\(f(x)\)的实现。 如果判别器被定义来使用一个逻辑sigmoid函数在输出层， 也就是 \(D(x)=\sigma(a(x))\), 那么 \(f(x)=-exp(a(x))\)。

这个练习来自Goodfellow (2014)的结果。 从这个练习中， 我们可以明白判别器估计密度的比值，可以用来计算不同的散度。

[最终修改于： 2017年6月15日]